Complementary and Supplementary Angles Worksheets⁚ A Comprehensive Guide
These worksheets offer a comprehensive guide to understanding complementary and supplementary angles, providing students with opportunities to practice identifying these angle pairs, finding unknown angles, and applying their knowledge to solve real-world problems. This guide includes printable worksheets, explanations of key concepts, and examples to enhance learning and understanding.
Introduction
In the realm of geometry, understanding angles is fundamental. Complementary and supplementary angles are essential concepts that form the building blocks for more complex geometric problems. These angles are defined by their specific relationships, creating a foundation for understanding geometric relationships and solving problems involving angles. Complementary and supplementary angles worksheets, often accompanied by answers, offer a structured and engaging way to explore these concepts and reinforce learning.
These worksheets typically present a variety of exercises designed to challenge students’ understanding of the definitions, properties, and applications of complementary and supplementary angles. They provide a platform for students to practice identifying angle pairs, calculating unknown angles, and applying these concepts to real-world scenarios. The inclusion of answers allows students to check their work and identify areas where they may need further review.
Whether used in a classroom setting or for independent study, complementary and supplementary angles worksheets serve as a valuable tool for solidifying understanding, building confidence, and developing a strong foundation in geometry. They offer a structured and interactive approach to learning, making the study of angles more engaging and effective.
What are Complementary and Supplementary Angles?
Complementary and supplementary angles are two fundamental concepts in geometry that describe the relationship between pairs of angles based on their sum. Understanding these relationships is crucial for solving problems involving angles, particularly in geometry and trigonometry.
Complementary angles are two angles whose measures add up to 90 degrees. Imagine a right angle, which measures 90 degrees. If you divide that right angle into two smaller angles, those two angles would be complementary. For example, a 30-degree angle and a 60-degree angle are complementary because 30 + 60 = 90. Complementary angles don’t have to be adjacent (next to each other), but they can be.
Supplementary angles, on the other hand, are two angles whose measures add up to 180 degrees. Think of a straight line, which measures 180 degrees. If you divide that straight line into two angles, those two angles would be supplementary. For instance, a 120-degree angle and a 60-degree angle are supplementary because 120 + 60 = 180. Like complementary angles, supplementary angles don’t have to be adjacent, but they can be.
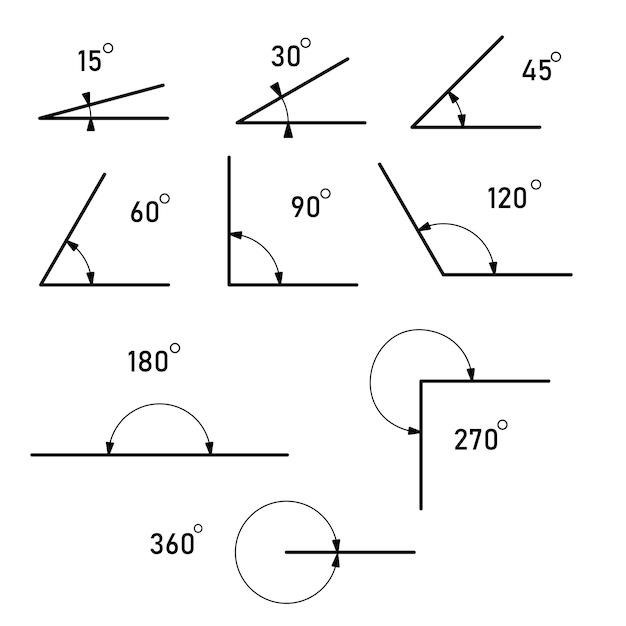
Types of Angles
Angles are classified based on their measure, and understanding these classifications is essential for working with complementary and supplementary angles. Here are some key types of angles⁚
- Acute Angle⁚ An acute angle measures less than 90 degrees. It’s a sharp angle, like the corner of a square or a triangle.
- Right Angle⁚ A right angle measures exactly 90 degrees. It’s formed by two perpendicular lines and is represented by a small square in the corner.
- Obtuse Angle⁚ An obtuse angle measures more than 90 degrees but less than 180 degrees. It’s a wide angle, like the corner of a table or a door slightly ajar.
- Straight Angle⁚ A straight angle measures exactly 180 degrees. It forms a straight line.
- Reflex Angle⁚ A reflex angle measures more than 180 degrees but less than 360 degrees. It’s a large angle that turns more than halfway around a circle.
These angle classifications help us understand the relationships between angles and make it easier to identify complementary and supplementary pairs.
Complementary Angles
Complementary angles are a special pair of angles that, when added together, result in a right angle (90 degrees). Imagine two angles forming a perfect corner of a square or a rectangle – that’s a visual representation of complementary angles. One angle might be smaller, while the other is larger, but they always add up to 90 degrees.
Here’s a simple way to remember complementary angles⁚ “C” comes before “S” in the alphabet, and 90 comes before 180. This helps you associate complementary angles with 90 degrees.
For example, if one angle is 30 degrees, its complementary angle would be 60 degrees (30 + 60 = 90). You can use this knowledge to find unknown angles in problems involving complementary angles.

Complementary angles are often found in geometric shapes like triangles and squares, where the angles within the shape add up to specific degrees. Understanding complementary angles is crucial for solving various geometric problems.
Supplementary Angles
Supplementary angles are another fascinating pair in the world of angles. They form a straight line, which means they add up to 180 degrees. Think of it like a straight road – the two angles together create a straight path.
One angle might be acute (less than 90 degrees), while the other is obtuse (greater than 90 degrees), but their combined measure will always equal 180 degrees. For instance, if one angle is 120 degrees, its supplementary angle would be 60 degrees (120 + 60 = 180).
You can think of supplementary angles as “supplementing” each other to form a straight line. They often appear in situations where two angles create a linear pair, meaning they share a common side and vertex (the point where two lines meet).
Understanding supplementary angles is crucial for working with various geometric shapes, solving problems involving angles on a line, and even grasping concepts like parallel lines. These concepts are essential for understanding and applying geometry in various fields.
Worksheet Examples
To solidify your understanding of complementary and supplementary angles, let’s look at some examples of worksheet problems you might encounter⁚
Problem 1⁚ Two angles are complementary. One angle measures 35 degrees. What is the measure of the other angle?
Solution⁚ Since the angles are complementary, their sum is 90 degrees. Subtract 35 degrees from 90 degrees to find the measure of the other angle⁚ 90 ⎻ 35 = 55 degrees.
Problem 2⁚ Two angles are supplementary. One angle measures 110 degrees. What is the measure of the other angle?
Solution⁚ Supplementary angles add up to 180 degrees. Subtract 110 degrees from 180 degrees to find the measure of the other angle⁚ 180 ─ 110 = 70 degrees.
Problem 3⁚ An angle measures 4x degrees. Its supplement measures (x + 20) degrees. Find the value of x.
Solution⁚ Since the angles are supplementary, their sum is 180 degrees. Set up an equation⁚ 4x + (x + 20) = 180. Combine like terms⁚ 5x + 20 = 180. Subtract 20 from both sides⁚ 5x = 160. Divide both sides by 5⁚ x = 32.
These are just a few examples of the types of problems you might encounter in complementary and supplementary angles worksheets. By working through various examples, you’ll gain confidence in identifying and applying these angle relationships.
Complementary Angle Worksheets
Complementary angle worksheets are designed to help students grasp the concept of complementary angles, which are two angles that add up to 90 degrees. These worksheets often present various problems that challenge students to identify complementary angles, calculate the measure of a missing angle, and solve problems involving complementary angles in real-world scenarios.
Here are some common types of problems found in complementary angle worksheets⁚
- Identifying Complementary Angles⁚ Students are presented with pairs of angles and asked to determine if they are complementary.
- Finding Missing Angle Measures⁚ One angle of a complementary pair is given, and students are asked to calculate the measure of the other angle;
- Algebraic Expressions⁚ Problems involve algebraic expressions where students need to solve for an unknown variable representing an angle measure.
- Word Problems⁚ Real-world scenarios involving complementary angles are presented, requiring students to apply their understanding to solve the problem.
Complementary angle worksheets are a valuable tool for reinforcing the concept of complementary angles and providing students with practice in applying this knowledge to various problem-solving situations.
Supplementary Angle Worksheets
Supplementary angle worksheets provide students with a focused platform to explore and practice the concept of supplementary angles. These worksheets typically present a variety of problems designed to enhance understanding and proficiency in working with supplementary angles, which are two angles that add up to 180 degrees.
Here’s a glimpse into the types of problems commonly encountered in supplementary angle worksheets⁚
- Identifying Supplementary Angles⁚ Students are given pairs of angles and tasked with identifying whether they are supplementary.
- Determining Missing Angle Measures⁚ One angle of a supplementary pair is provided, and students are required to calculate the measure of the other angle.
- Algebraic Expressions⁚ Problems involve algebraic expressions where students need to solve for an unknown variable representing an angle measure within a supplementary angle pair.
- Real-World Scenarios⁚ Word problems are included, presenting real-life situations involving supplementary angles, challenging students to apply their understanding to find solutions.
Supplementary angle worksheets serve as a valuable resource for solidifying students’ understanding of supplementary angles and providing them with ample practice in applying this concept to various problem-solving situations.
Combining Complementary and Supplementary Angles
Combining complementary and supplementary angles in worksheets creates more complex and engaging problems for students. These problems challenge students to synthesize their understanding of both angle relationships and apply them in a single scenario. Here’s how these combined problems might appear⁚
Example⁚ A problem might provide the measure of one angle and ask students to determine the measures of its complement and supplement. This requires students to use both angle relationships to solve the problem.
Another example⁚ A worksheet might involve a diagram with multiple angles, some of which are complementary and others supplementary. Students would need to analyze the diagram, identify the angle relationships, and then solve for unknown angle measures.
Combining complementary and supplementary angles in worksheets helps students develop a deeper understanding of these concepts and their interrelationship. These problems encourage critical thinking and problem-solving skills as students apply their knowledge to more complex situations.
Real-World Applications
Complementary and supplementary angles are not just abstract mathematical concepts; they have practical applications in various real-world scenarios. These concepts play a crucial role in fields like architecture, engineering, and construction.
For example, architects use complementary and supplementary angles when designing buildings. They ensure that windows and doors are positioned at angles that allow for optimal sunlight and ventilation. Engineers rely on these concepts when designing bridges, roads, and other structures, ensuring stability and safety. In construction, understanding these angle relationships is essential for accurately cutting materials and assembling structures.
Beyond these professional fields, everyday situations involve complementary and supplementary angles. Think about the angle of a ladder against a wall or the way a door swings open. By incorporating these real-world examples into worksheets, students can see the practical relevance of these concepts and better understand their application in the world around them.
Benefits of Using Worksheets
Complementary and supplementary angles worksheets offer a multitude of benefits for students learning about these concepts. These worksheets provide a structured and engaging way to practice and reinforce learning, leading to a deeper understanding of the concepts.
Firstly, worksheets provide a visual representation of the concepts, allowing students to visualize and manipulate angles. This visual approach enhances comprehension and helps them grasp the relationships between complementary and supplementary angles. Secondly, these worksheets offer a variety of practice problems, allowing students to apply their knowledge in different contexts. This repetition and application solidify their understanding and build confidence in their problem-solving skills.
Thirdly, worksheets provide immediate feedback, allowing students to assess their understanding and identify areas where they need further practice. This self-assessment fosters independent learning and helps students take ownership of their learning process. Finally, worksheets can be used for individual practice, group work, or peer tutoring, promoting collaboration and active learning. In conclusion, these worksheets are valuable tools for educators and students alike, contributing to a more engaging and effective learning experience.
In conclusion, complementary and supplementary angles worksheets play a crucial role in enhancing the understanding of these fundamental geometric concepts. Through engaging practice problems, visual aids, and opportunities for self-assessment, these worksheets empower students to develop a solid foundation in angle relationships.
Whether used for individual study, classroom activities, or peer tutoring, these worksheets provide a valuable resource for both educators and students. By fostering a deeper comprehension of complementary and supplementary angles, these worksheets lay the groundwork for further exploration of geometry and related concepts, ultimately contributing to a more successful and enriching learning experience.
These worksheets provide a valuable tool for educators and students alike, contributing to a more engaging and effective learning experience. By embracing these resources, students can confidently navigate the world of geometry and build a strong foundation for future mathematical endeavors.